¿Cómo calcular la altura de 2 triángulos semejantes con 2 ángulos conocidos?

Publicadas por בן האלוהים el julio 24, 2019

Triángulo rectángulo

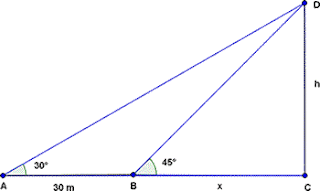
Hallar en valor de h

Resolución:

Ambos triángulos poseen en común es la altura h.

El angulo de inclinación se calcula así:

$\theta =\tan^{-1}\left ( \frac{y}{x} \right )$ siendo y = h

Ahora:

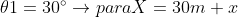
$\theta 1=30^{\circ } \rightarrow para X=30m +x$

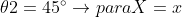
$\theta 2=45^{\circ } \rightarrow para X= x$

$30^{\circ }= \tan^{-1}\left ( \frac{y}{30+x} \right ) \wedge 45^{\circ }=\tan^{-1}\left ( \frac{y}{x} \right )$

Se despeja y de ambas ecuaciones:

$\left ( 30+x \right )\frac{\sqrt{3}}{3}=y \wedge x=y$

igualamos

$\left ( 30+x \right )\frac{\sqrt{3}}{3}=x$

despejamos x

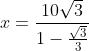
$x=\frac{10\sqrt{3}}{1-\frac{\sqrt{3}}{3}}$

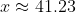
$x\approx 41.23$

Como en el triangulo interno y = x , la altura que buscamos es igual:

h= 41.23

Si comprobamos la altura del triangulo externo debe ser igual.

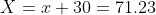
$X=x+30=71.23$

$\cos \left ( 30^{\circ } \right ). Hip= x$

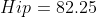
$Hip = 82.25$

$y=\sin \left ( 30^{\circ } \right ).Hip$

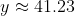
$y\approx 41.23$

La misma altura.

Comentarios

SERVICIOS

PROGRAMACIÓN

Desarrollo de programas en Python, incluyendo la creación de scripts automatizados y aplicaciones web. Gestión y administración de bases de datos SQL y SQLite, asegurando la integridad y eficiencia de los datos. Programación en Lenguaje C y C++, con énfasis en la optimización de rendimiento y el desarrollo de sistemas embebidos. Diseño y estilización de páginas web utilizando CSS para crear interfaces de usuario atractivas y funcionales.

DESARROLLO DE APP

Las aplicaciones no solo mejoran la visibilidad de cualquier idea, sino que también permiten una mayor interacción y alcance con el público objetivo. Al proporcionar una plataforma accesible y fácil de usar, las aplicaciones logran un impacto significativo, facilitando la comunicación y promoviendo la adopción de nuevas ideas y soluciones.

Odoo ERP

Gestión, modificación y creación de nuevos campos para Odoo ERP. El sistema ERP de Odoo es un software de planificación de recursos empresariales que se utiliza en toda la empresa para la gestión de procesos comerciales. Es el software de gestión empresarial perfecto para pequeñas, medianas y grandes empresas de cualquier sector.

El ERP de Odoo es un software ERP todo en uno que ofrece muchas funciones en forma de aplicaciones que se pueden activar en función de las necesidades empresariales. Odoo cubre una amplia gama de aplicaciones y módulos como CRM, Ventas, Desarrollo, Comercio electrónico, POs, Gestión de compras, Gestión de proyectos, Fabricación, Gestión de almacenes, Gestión de contabilidad y finanzas, Recursos humanos, etc. Hay diferentes aplicaciones disponibles en función de las verticales de negocio que pueden ser instaladas y utilizadas por las empresas.

CIBERSEGURIDAD

La información es un recurso sumamente valioso y su protección es crucial. Por esta razón, es fundamental evitar que cualquier tercero no autorizado tenga acceso a datos sensibles. La seguridad de la información debe ser una prioridad para garantizar la confidencialidad, integridad y disponibilidad de los datos, protegiendo así tanto a individuos como a organizaciones de posibles amenazas y vulnerabilidades.

DISEÑO WEB

Tener tu propio sitio web es como disponer de un catálogo digital de tus ideas o productos, accesible en todo momento para clientes potenciales. Un sitio web te permite mostrar tu oferta de manera profesional y atractiva, facilitando la conexión con tu audiencia y ampliando tu alcance. En el mundo digital actual, no puedes permitirte estar sin una página web, ya que es una herramienta esencial para el crecimiento y éxito de cualquier proyecto o negocio.

DESCARGAR

DESCARGAR MP3 DE YOUTUBE

DKESCORPIO

Buscar este blog

¿Cómo calcular la altura de 2 triángulos semejantes con 2 ángulos conocidos?

Comentarios

Publicar un comentario

SERVICIOS